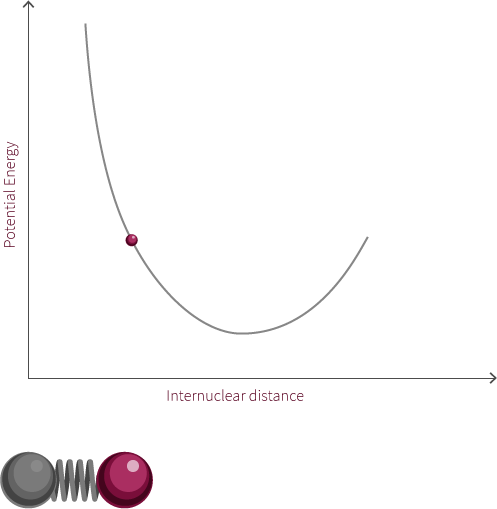
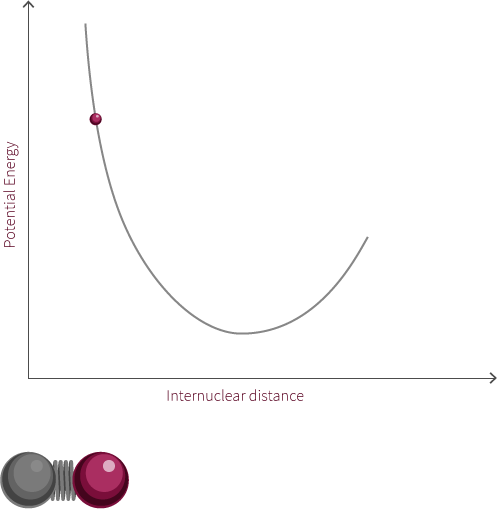
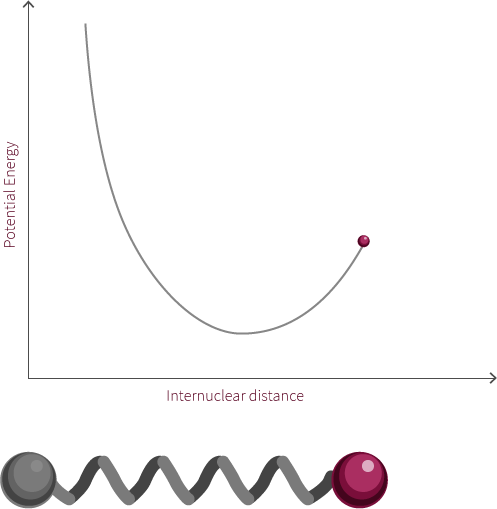
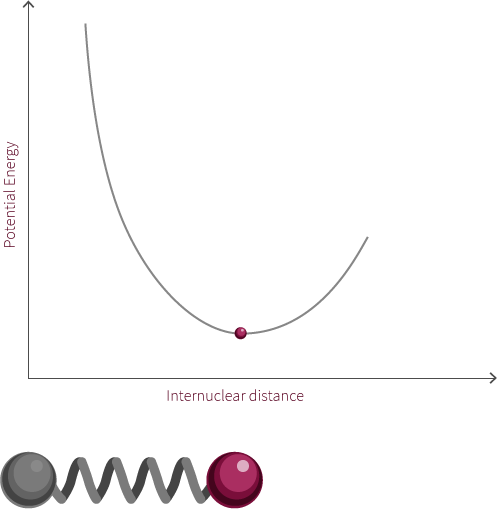
To address the quantum quantum nature of molecules we add discrete energy levels to the Morse potential curve. The discrete energy levels are denoted by horizontal lines that represent the vibrational and rotational energy state of the molecule.
Morse Potential
Both rotation and vibration are quantized, which leads to discrete energy levels. At room temperature, the lowest vibrational and rotational levels are the ones most commonly occupied. The different vibrational states are linked to the oscillatory motion of bonds.
The vibrational state of the diatomic molecule refers to the frequency at which the atoms oscillate. The frequency of molecular vibrations are in the order of 10-12 to 10-14 Hz. In this simple molecule, the only vibration mode available is along the bond. More complicated molecules have many types of vibration and stretching modes.
Only certain frequencies are allowed by selection rules for the observed bond oscillation, and is similar to what is observed with standing waves. The fundamental frequency forms a standing wave with a two nodes and a single anti-node. Only specific multiples of the fundamental frequency will result in standing waves (1f, 2f, 3f,.., etc.). Hence, there are only discrete frequencies for standing waves, just like there are discrete vibration modes for bond stretching.
Standing waves
Adjust the frequency of the vibration to the left by clicking the π orbitals, the vibration level directly or the selector. What happens to the potential energy? What happens to the appearance of the string? What happens to the string at the harmonic frequencies?